Ilan Bernstein

Why?

I was recently thinking about pie, as one does on a Sunday afternoon, and I thought about the thing on top of a pie. Apparently, the “thing on top of a pie” is called a lattice crust.

A lattice crust!

How?

So, what does a lattice crust have to do with pi? Everything! I started to think about the places where the lattice crust and the and the pie crust meet (as I was wondering how bakers merged the two. Maybe score and slip like in pottery?), and this made the following diagram appear in my head.

Remove the pie, add blue, and you get the EU!

Are you starting to see it? I’ll give you a hint: think triangles!

And just like that, pie becomes pi.

Together, we will ignore the hand wavey way we got here, and just focus on the math from now on! Now here was my idea: we could calculate the height of the triangle by using the Pythagorean theorem. And by plugging in many values for $x$ , we could find find the height (which I’ll call $y$ )! Now over time, we can generate enough points to create a quarter of a circle (all the other points could be found by negating all my $y$ and $x$ values, but I won’t do this for reasons later revealed).

And we a perimeter emerges!

Now that we have a list of points making up the entire circle, we can calculate the distance between neighboring points, and add them up to find the perimeter (or rather circumference as the distance between our $x$ values, also known as $\Delta x$ , approaches 0!)

Pi is defined is, $\pi=\frac{C}{d}$ , and we know that $d=2$ since $r=1$ , therefore, we can say that $\pi=\frac{C}{2}$

Since we know we can calculate $\frac{C}{4}$ right now, we can simply plug that into our formula to find $\pi$ !

And just like that, we are ready to start programming!

The Program

I’ve decided to write this in C++ to pump out all the speed I could get, but ported it to Python for the sake of simplicity here. Just some fair warning, I do not like Python, and have not programmed in it for years now, so if I do something inefficiently you know who to blame!

First, let’s calculate all of our points:

from math import sqrt

points = []

NUM_SEGMENTS = 10000000

for unscaled_x in range(0, NUM_SEGMENTS):
    x = unscaled_x / NUM_SEGMENTS
    y = sqrt(1 - x**2)
    points.append((x, y))

Now we can find the distance between each consecutive point:

distances = []

for i in range(len(points) - 1):
    (x_1, y_1) = points[i]
    (x_2, y_2) = points[i + 1]
    
    distance = sqrt((x_2 - x_1)**2 + (y_2 - y_1)**2)

    distances.append(distance)

Finally, let’s print them out to see our output!

print(sum(distances) * 2)

And we can finally see that our output is just around 3.14. Isn’t that awesome! To bring up the accuracy of our answer at the cost of speed, we can also increase the number of NUM_SEGMENTS.

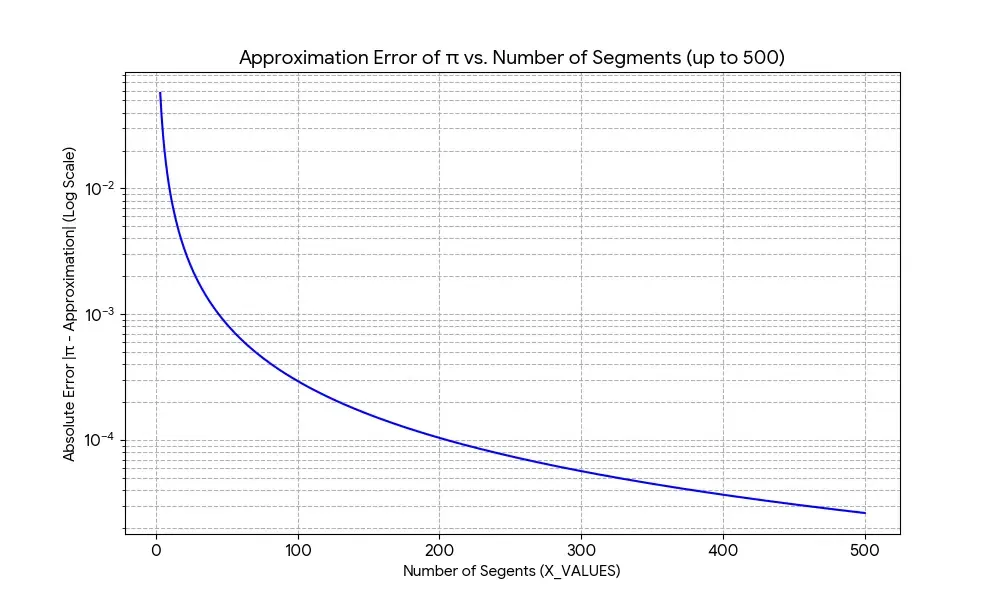
Just one more thought

If you got bored a while ago, feel free to skip this section, but I think its the coolest part!

I was thinking about this problem for a while after writing this post, and had a sudden epiphany. When $x$ is around $0$ our $y$ -values change significantly less than when $x$ is around $1$ . This means we should be able to more efficiently estimate $\pi$ by changing our $\Delta x$ to be non-constant. Quickly, I’ll show the code I used to do this:

NUM_SEGMENTS = 10000000

points_quadratic = []
for i in range(NUM_SEGMENTS + 1):
  u = i / NUM_SEGMENTS
  x = 1 - (1 - u)**2

  if 1 - x**2 >= 0:
    y = math.sqrt(1 - x**2)
    points_quadratic.append((x, y))

distances_quadratic = []

for i in range(len(points_quadratic) - 1):
  (x1, y1) = points_quadratic[i]
  (x2, y2) = points_quadratic[i + 1]
  distance = math.sqrt((x2 - x1)**2 + (y2 - y1)**2)
  distances_quadratic.append(distance)

print(sum(distances) * 2)

This code calculates x using a quadradic. If you’re wondering how it looks, I invite you to graph the quadradic ( $x=1 - (1-u)^2$ ) on Desmos, and even try to graph the derivative if you’re wondering about how much $x$ is changing for each $u$ . I have yet to find a more efficient equation (if there is one!), but if anyone finds one please do send it to me!

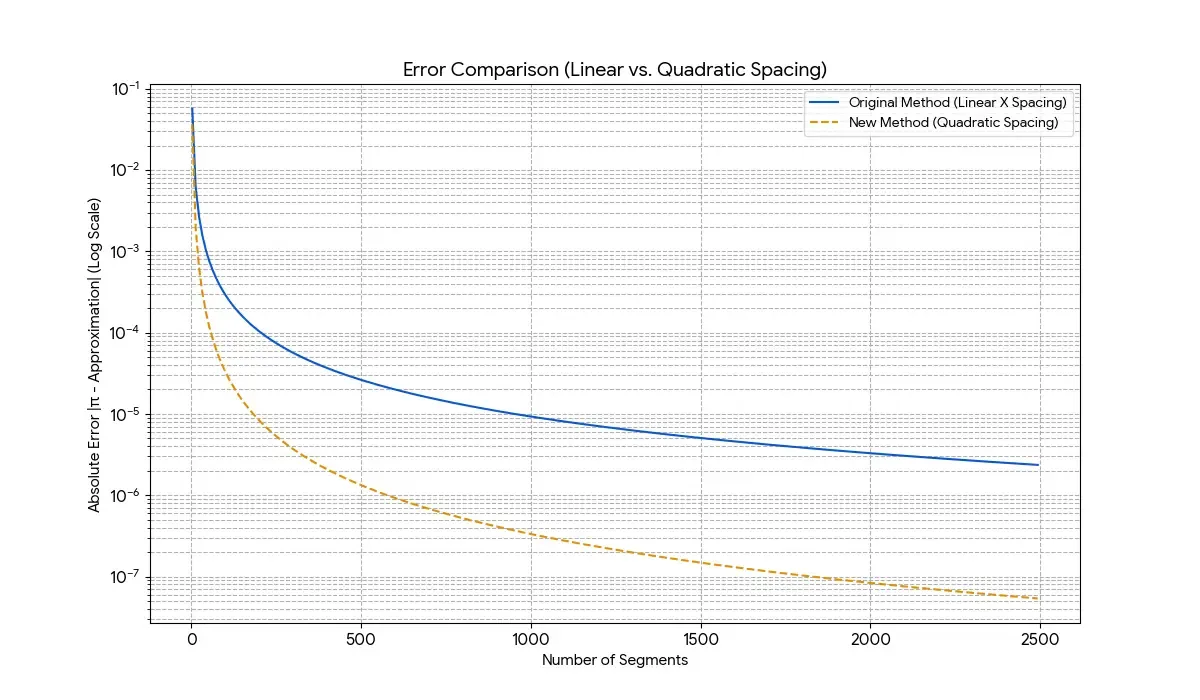3 orders of magnitude!!!

Conclusion

Now you can calculate pi all on your own! I smell a pie fresh out of the oven, so I gotta go, but I hope you enjoyed!

Have a good morning, evening, or night,
~Ilan Bernstein